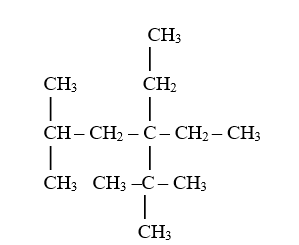
1. Gugus alkil
Gugus alkil senyawa alkana yang kehilangan satu atom H. Alkil mempunyai rumus umum CnH2n+1. Penamaan alkil sesuai nama alkananya, tetapi akhiran –ana diganti –il
Gambar 8. Gugus Alkil
Tabel 2. Struktur, Rumus Molekul dan Nama Beberapa Alkil.
Struktur | Rumus Molekul | Nama |
CH3− | CH3− | Metil |
CH3− CH2− | C2H5− | Etil |
CH3− CH2− CH2− | C3H7− | Propil |

| C3H7− | Isopropil |
CH3− (CH2)2− CH2− | C4H9− | Butil |
| C4H9− | Isobutil |
CH3− (CH2)3− CH2− | C5H11− | Pentil//amil |
CH3− (CH2)4− CH2− | C6H13− | Heksil |
CH3− (CH2)5− CH2− | C7H15− | Heptil |
CH3− (CH2)6− CH2− | C8H17− | Oktil |
CH3− (CH2)7− CH2− | C9H19− | Nonil |
CH3− (CH2)8− CH2− | C10H21− | Dekil |
2. Aturan penamaan senyawa alkana
a. alkana rantai lurus (tidak bercaban
alkana diberi nama sesuai jumlah atom-nya diberi awalan n- (normal).
Contoh :
Tontonlah video contoh cara penamanaa alkana rantai lurus di bawah ini ya👇
b. Aturan penamaan senyawa alkana rantai bercabang
1) Nama alkana dipilih berdasarkan rantai C terpanjang (rantai utama/rantai induk).
2) Atom-atom C yang terletak di luar rantai utama merupakan rantai cabang atau gugus alkil.
Contoh : CH3− : metil
CH3 – CH2− : etil
~ Cabang yang sama disebut jadi satu dengan diberi awalan :
1 = mono 2 = di
3 = tri 4 = tetra
5 = penta 6 = heksa
~ Cabang yang tidak sama disebut sesuai urutan abjad
Contoh : etil disebut lebih dahulu daripada metil
3) Penomoran atom C pada rantai utama dimulai dari ujung yang terdekat dengan cabang.
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Butana
Ø Gugus alkil : metil
Ø Gugus akil terletak pada atom C nomor 2
Ø Nama adalah : 2-metilbutana
4) Alkil-alkil yang tidak sejenis dituliskan berdasarkan urutan abjad (butil, etil, iso, metil, propil).
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Pentana
Ø Gugus alkil : etil dan metil
Ø Gugus akil terletak pada atom C nomor 2 dan nomor 3
Ø Nama senyawa adalah : 3-etil-2-metilbutana
5) Alkil-alkil sejenis penulisannya digabung dengan diberi awalan di-(2), tri-(3), tetra-(4), penta-(5), dan seterusnya.
Karena ada dua alkil sejenis yaitu metil maka penulisannya menjadi dimetil.
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Pentana
Ø Terdapat dua gugus alkil -CH3 : metil
Ø Gugus alkil terletak pada atom C nomor 2 dan 3
Ø Nama senyawa adalah : 2,3-dimetilpentana
6) Apabila salah satu atom C pada rantai utama mengikat dua gugus alkil, penulisan nomornya harus diulang.
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Pentana
Ø Terdapat dua gugus alkil -CH3 : metil
Ø Gugus alkil terletak pada atom C nomor 2 dan 2
Ø Nama senyawa adalah : 2,2-dimetilpentana
7) Alkil yang mengandung atom C terbanyak terikat pada atom C rantai utama dengan nomor terkecil.
5CH3 −4CH2–3CH–(CH2–CH3)
│
1CH3−2CH–(CH3)
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Pentana
Ø Terdapat dua gugus alkil : metil dan etil
Ø Gugus metil terletak pada atom C nomor 2 dan gugus etil terletak pada atom C nomor 3.
Ø Nama senyawa adalah : 3-etil-2-metilpentana bukan 3-etil-4,4-dimetilpentana
8) Apabila terdapat beberapa alternatif rantai terpanjang, dipilih yang mengandung cabang sebanyak mungkin.
Penamaan senyawa tersebut adalah :
Ø Rantai C terpanjang 5 : Pentana
Ø Terdapat dua gugus alkil : Metil dan Etil
Ø Gugus metil terletak pada atom C nomor 2 dam 2 dan gugus etil terletak pada atom C nomor 3.
Ø Nama senyawa adalah : 3-etil-2,2-dimetilpentana bukan 3-tersierbutilpentana
Tontonlah video contoh penamaan alkana rantai bercabang di bawah ini ya👇
2.8.2 Tata Nama Alkena
Alkena merupakan senyawa hidrokarbon yang memiliki ikatan rangkap dua pada rantai karbonnya. Dalam rantai karbon alkena terdapat satu ikatan rangkap dua dan memiliki rumus umum alkena adalah CnH2n.
Nama-nama alkena diambil dari nama alkana tetapi akhiran–ana diganti–ena. Tabel 3 menyajikan nama senyawa alkena suku kedua hingga sepuluh.
Tabel 3. Rumus Struktur, Rumus Molekul dan Nama Senyawa Alkena
Rumus Struktur | Rumus Molekul | Nama Kimia |
H2C = CH2 | C2H4 | Etena |
H2C = CH − CH3 | C3H6 | Propena |
H2C = CH − CH2 − CH3 | C4H8 | 1-butena |
H2C= CH – (CH2)2 − CH3 | C5H10 | 1-pentena |
H2C= CH – (CH2)3 − CH3 | C6H12 | 1-heksena |
H2C= CH – (CH2)4 − CH3 | C7H14 | 1-heptena |
H2C= CH – (CH2)5 − CH3 | C8H16 | 1-oktena |
H2C= CH – (CH2)6 − CH3 | C9H18 | 1-nonena |
H2C= CH – (CH2)7 − CH3 | C10H20 | 1-dekena |
Aturan pemberian nama alkena rantai lurus sebagai berikut :
1. Rantai utama adalah rantai terpanjang yang mempunyai ikatan rangkap dua.
2. Penomoran rantai utama dimulai dari atom C yang paling dekat dengan ikatan rangkap dua.
Tontonlah video contoh penamaan alkena rantai lurus di bawah ini ya👇
3. Penulisan letak ikatan rangkap dua diawali oleh nomor atom C yang mengikat ikatan rangkap dua tersebut.
Contoh : 1CH₂=2CH−3CH₂−4CH₂−5CH₃ 1-pentena
Tontonlah video contoh penamaan alkena rantai bercabang di bawah ini ya👇
4. Pada alkena bercabang, pemberian nama senyawa seperti pada alkana.
5. Jika alkena mengandung dua ikatan rangkap dua, senyawa alkena diberi nama dengan akhiran –diena. Jika mengandung tiga ikatan rangkap dua dinamakan–triena, dan seterusnya. Berdasarkan letak ikatan rangkap dua dalam rantai C-nya, alkena mempunyai tiga kemungkinan letak ikatan rangkap dua sebagai berikut.
a. Kumulatif, jika letak ikatan rangkap dua berurutan di satu sisi rantai karbon.
1CH₂=2CH=3CH–4CH–5CH₃ → 1,2 pentadiena
b. Konjugatif, jika letak ikatan rangkap dua selang-seling dengan ikatan tunggal.
1CH₂= 2CH–3CH=4CH–5CH₃ → 1,3 pentadiena
c. Terisolasi, jika letak ikatan rangkap dua terikat pada atom C primer di ujung rantai.
1CH₂=2CH–3CH–4CH–5CH–6CH2 → 1,5-heksadiena
6. Selain nama IUPAC, pada alkena juga dikenal nama trivial, misalnya etena = etilena, propena = propilena.
2.8.3 Tata Nama Alkuna
Alkuna adalah senyawa hidrokarbon yang mempunyai satu ikatan rangkap tiga antar atom C pada rantai karbonnya. Oleh karena terdapat satu ikatan rangkap tiga pada rantai karbonnya, alkuna menjadi kekurangan dua atom H dibanding alkena sehingga rumus umum alkuna adalah CnH2n–2. Nama-nama alkuna diambil dari nama alkana, tetapi akhiran –ana diganti –una.
Tabel 4. Rumus Molekul, Rumus Struktur dan Nama Beberapa Senyawa Alkuna
Rumus Molekul | Rumus struktur | Nama IUPAC | Nama Trivial |
C2H2 | CH ≡ CH | Etuna | Asetilena |
C3H4 | CH ≡ C− CH3 | Propuna | Metil asetilena |
C4H6 | CH ≡ C− CH2− CH3 | 1-butuna | Etil asetilena |
CH3− C ≡ C − CH3 | 2-butuna | 1,1-dimetilasetilena |
1. Aturan Tata nama alkuna
Cara pemberian nama pada alkuna sama dengan alkena. Perkecualian untuk trivial C2H2 adalah asetilena. Akhiran –ena dari nama asetilena bukan berarti sama dengan akhiran –ena pada senyawa alkena. Ingat, asetilena merupakan nama trivial, bukan nama IUPAC. Berdasarkan rumus umumnya, alkuna merupakan isomer fungsi dari alkadiena.
Contoh :
*Rantai lurus
1CH ≡ 2C− 3CH3 CH2 = C = CH2
1-propuna (C3H4) 1,2-propadiena (C3H4)
Jadi, untuk rumus molekul C3H4 kemungkinan propuna atau 1,2-propadiena.
Silahkan untuk menonton video contoh penamaan alkuna rantai lurus di bawah ini👇
*Rantai bercabang
3-metil-1-butuna
Tontonlah video contoh penamaan alkuna rantai bercabang di bawah ini ya👇
Latihan soal :
1. Nama IUPAC yang tepat untuk senyawa berikut ini adalah.........
a. 3-tersierbutil-3-etil-1,1-dimetilpentana
b. 4-etil-1-metil-4-tersierbutilheksana
c. 4-tersierbutil-4-etil-1-metilheksana
d. 4,4-dietil-2,5,5-trimetilheksana
e. 3,3-dietil-2,2,5-trimetilheksana
2. Rumus struktur dari 6-etil-4-isobutil-2,2-dimetil-1-oktena adalah..........